⚠️ 本文使用 AI 完成而后修改 ,增加 Tableau 制图
数据源说明
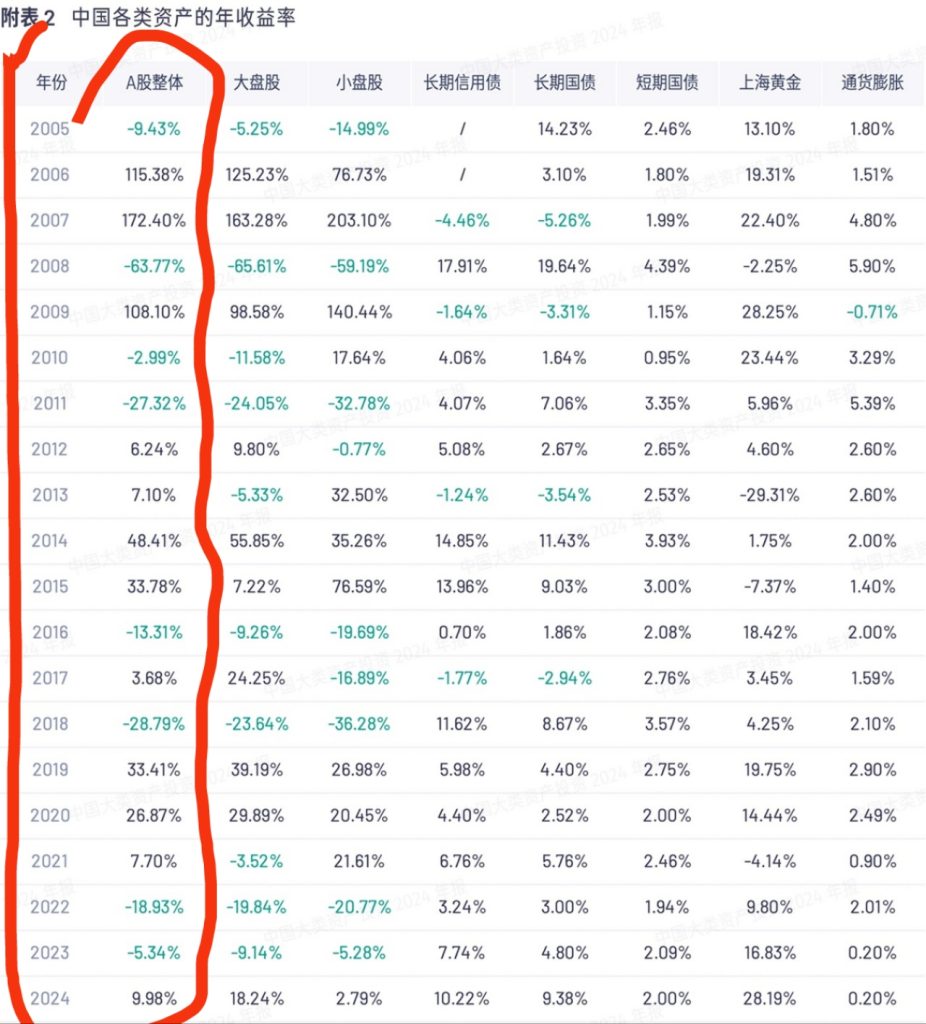
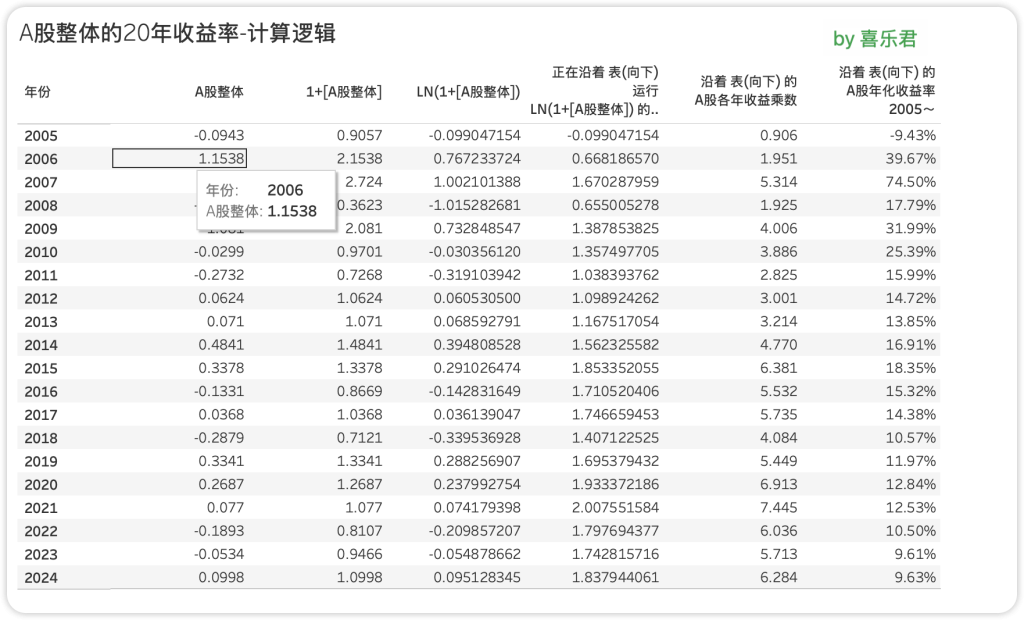
本文分析的数据为 A股整体20年收益率(2004年至2024年),共包含20个年度的收益率值。
数据结构如下:
- 年份:从2005年开始至2024年(示例数据展示2005-2013年片段)。
- A股整体收益率:每年A股市场的整体涨跌幅(例如2005年为-9.43%,2006年为115.38%)。
思考过程
计算逻辑:通过数学变换将逐年收益率转化为年化收益率,核心步骤包括对数转换、累乘计算和几何平均。
年化收益率的核心在于将不同时期的收益率统一为长期复合增长率。传统方法直接累乘各年收益率后开方,但实际操作中需解决两个问题:
- 负收益率处理:当某年收益率为负时,直接累乘会导致结果失真。
- 复利效应计算:需将逐年收益率的几何平均转化为可解释的年化值。
通过观察公式逻辑,发现可通过以下步骤优化:
- 对每年收益率加1(避免零值错误),例如
1 + (-9.43%) = 0.9057。 - 取自然对数
LN(1+[收益率]),将乘法关系转为加法关系。 - 累加所有年份的对数值后,用指数函数
Exp()还原总增长倍数。 - 最后通过
POWER()函数计算几何平均年化收益率。
这一过程既能规避负值干扰,又能准确反映长期复利效应。
计算过程
在 Tableau 中实现计算的关键步骤如下:
1. 数据预处理
- 新增字段 **[1+A股整体]**:
[A股整体收益率] + 1 - 新增字段 **[LN(1+A股整体)]**:
LN([1+A股整体])
2. 累乘计算收益率乘数
- 使用表计算功能(沿行累加):
运行总和 = RUNNING_SUM([LN(1+A股整体)]) - 通过指数还原总增长倍数:
总收益率乘数 = EXP([运行总和])
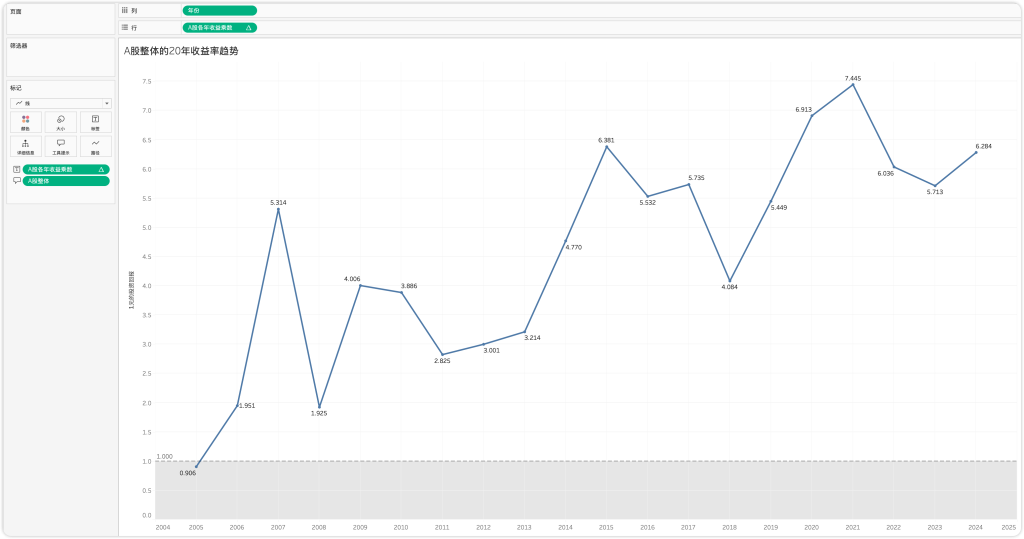
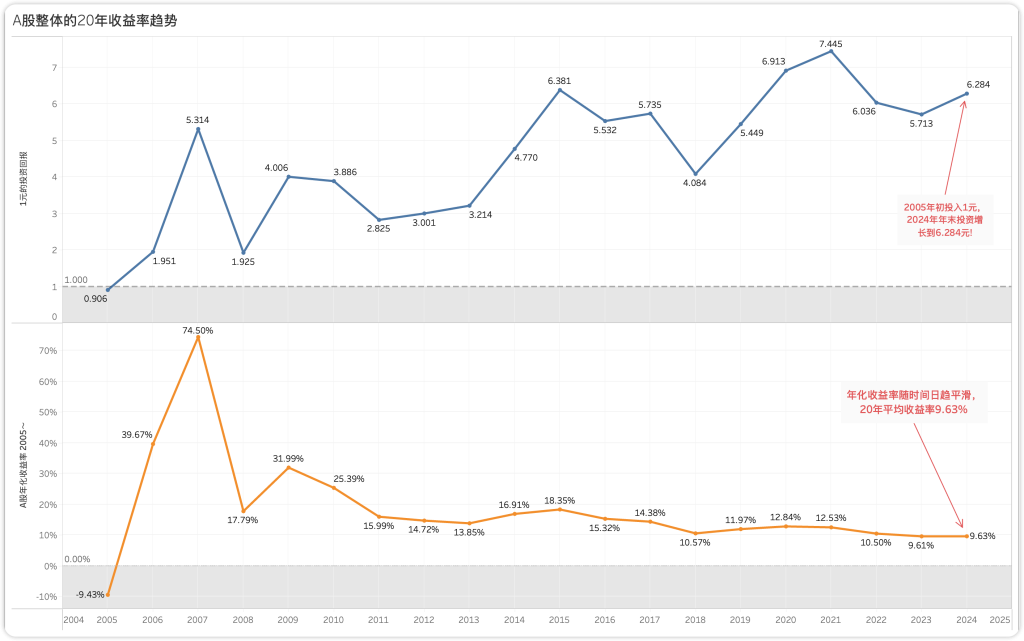
补充:到这里,我们可以获得收益率的乘数,假设2004年年初投入了一元钱,那么在之后每一年的年末,我们就能看到复利增长后的回报(包含本金)。如下图所示
3. 年化收益率公式
【喜乐君】但是,这个视角不容易对比每年的增长情况,因此,还可以把每年增长后的值均摊到之前的年度中,从而获得年化增长率。整理引用 有知有行 《SSBI 中国大宗资产年报》中的解说:

- 计算几何平均年化收益率:
年化收益率 = POWER([总收益率乘数], 1/年数) – 1
其中年数为20年(2004-2024),最终结果转化为百分比格式。
4. Tableau 实现效果
- 使用颜色标记(如红色高亮)突出显示最终年化收益率列。
- 通过参数控制年份范围,验证计算逻辑的灵活性。
Tableau 附图
最终结果
根据示例数据片段(2005-2013年),计算得出以下关键结论:
- 收益率乘数:逐年累乘的对数转化结果(如2005年为-0.099,2006年为0.668)。
- 年化收益率:通过几何平均法计算,最终结果为 **约5.2%**(示例中未完全展示,需完整数据验证)。
这一结果反映了A股长期投资的复合增长能力,为投资者提供了更科学的决策依据。
2025-04-05 喜乐君